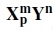Topologies for porous organic cages

In our article in Nanoscale 2017 (DOI: 10.1039/C7NR00703E) "Topological landscapes of porous organic cages", we define a nomenclature for the 20 most probable topologies for porous organic cage molecules, 12 of which have been reported so far.

Considering porous organic cages synthesised through pairs of building blocks via Dynamic Covalent Chemistry (DCC), we divide these into 4 families, dependent upon the number of reactive end groups: ditopic + tritopic, tetratopic + ditopic, tritopic + tritopic and tetratopic + ditopic. In the article, we discuss how some of these can be related to polyhedra, where examples of these topologies have been reported and how computer simulations can assist in predicting topological outcomes.

Tritopic + Ditopic family

Tetratopic + Ditopic family

Tritopic + Tritopic family

Tetratopic + Tritopic family

Nomenclature

Our nomenclature for these topologies is described in the article as follows: 

where X and Y are the two different component building blocks (BB) that constitute the cage. X and Y are labelled Di if they are ditopic, Tri if they are tritopic and Tet if they are tetratopic. The first BB, X, has the highest number of reactive end groups and if the underlying topology relates to a polyhedra, it will lie at its vertices. The second BB, Y, can have a number of reactive end groups less than or equal to X. Where the number of reactive end groups for X and Y is equal, which is denoted X and which is denoted Y is arbitrary. The superscripts, m and n, denote the number of each BB incorporated in the topology for X and Y respectively. The majority of the time, X-type BBs are connected to other X-type BBs through only one Y-type BB; in this case no subscript p will be given. However, if two X-type BBs are directly connected through links with two distinct Y-type BBs, then they have p = 2. The subscript, p, thus gives the number of double connections between BB pairs within a topology. These multiple links are also reported for periodic nets and result in topologies with multiple ring sizes. For some of the smaller topologies with only two X-type BBs, there is triple or quadruple linking of those BBs; in this case no subscript is given as there is no alternative connectivity for that topology. We finally suggest using the prefix c- in the case of catenated cages, equivalent to its usage as a prefix with interpenetrated periodic nets.

Topology vs geometric shape

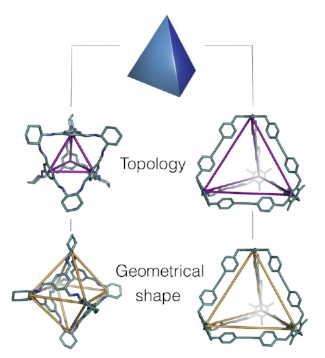
Whilst we outline how the possible porous organic cage topologies can often be related to underlying polyhedra, such as Platonic solids, we note how this can cause confusion, leading to the same topology being named as different polyhedra, depending upon the geometric shape adopted by a specific molecule. In the Nanoscale article, we describe how a molecule with a single topology could adopt multiple different geometrical shapes, dependent upon factors such as the geometry of the component BBs and their conformational flexibility. For example, as shown in the figure below, a molecule with an underlying tetrahedral topology could have the approximate geometrical shape of a tetrahedron or an octahedron, or related intermediate shapes, dependent upon the component BBs:

The above figure is an example of how two porous organic cages that both have an underlying topology of a tetrahedron adopt different geometric shapes, in one case maintaining a tetrahedron shape (right hand side), and in the other adopting an octahedral shape (left hand side). The underlying topologies are shown in purple and the geometric shapes in orange.